как совершенен Отец ваш Небесный
(Мф. 5:48)
Введение
Удивительно устроено познание человека. Даже когда набирается множество фактов, противоречащих или изменяющих выбранную человеком картину мира, он продолжает упорно следовать отжившей модели, не замечая того, что его усилия напрасны. Вместо того, чтобы повернуть, вернуться назад, осмыслить новые данные, изменить вектор движения, он начинает биться в гносеологическую стену в надежде ее проломить. А для оправдания этого безсмысленного действа он придумывает разные причины, модели, которые превращают эту гносеологическую стену либо в непреодолимое препятствие, либо в ничто, тем самым порождая надежду на осмысленность усилий. Человек либо успокаивается, и познание умирает, либо он превращается в пророка, свет истины которого не понимают окружающие.
Наглядный пример тому понимание и применение модели точки. А, по сути, это вопрос о правомерности используемых геометрических моделей, правил их преобразований, о границах применимости моделей действительности.
Если не понимать границ применимости моделей, то мы получаем такие абстракции, которые не только не ведут к истине, но уводят от нее.
Эквилибристика ума при решении тех или иных задач математики должна восприниматься только как эквилибристика ума, если в условиях задачи не оговорены граничные условия применения метода.
Например, представление о точке, как нульмерном объекте, сопряжено с противоречием непрерывности линии, которая состоит из множества точек. Это противоречие, например, приводит к тому, что отрезки разной длины по количеству точек равны между собой.
Поясню на примере.
Для этого нарисуем угол и две параллельные секущие. А, В, С, D – точки пересечения секущих со сторонами угла.
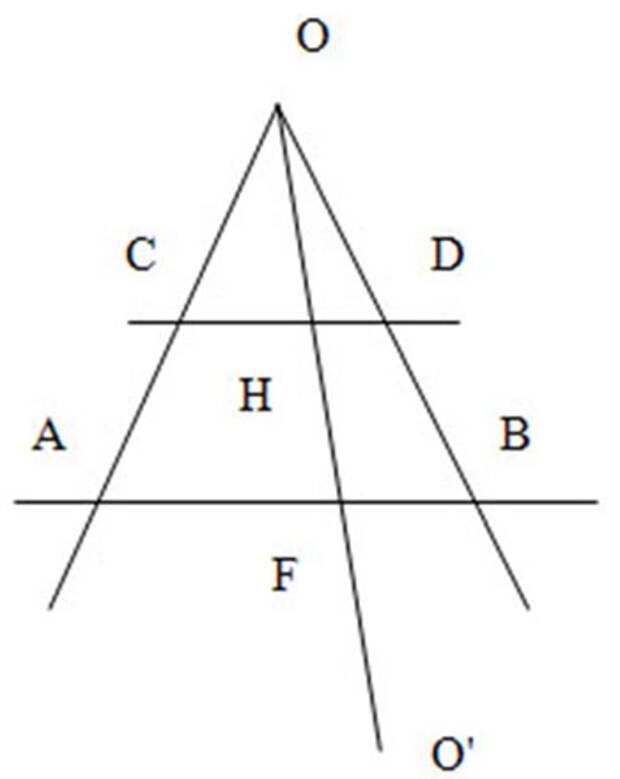
Через точки F и H на этих секущих проведем линию ОО’.
Тогда имеем следующую проблему.
Для любой точки на отрезке AF и на отрезке CH всегда найдется такая точка, что через них и точку О можно будет провести прямую. Иначе говоря, как бы, количество точек на AF и CH одинаково. Множества их равномощны, т.е. между точками этих двух отрезков можно установить взаимно однозначное соответствие. Но это будет справедливо для любого отрезка на любой секущей проведенной как угодно близко к точке О. С точки зрения счетных множеств длина AF равна CH. Этот наглядный парадокс, конечно, проистекает из противоречия в аксиоматике, когда из нульмерных непротяженных объектов, каким является математическая точка, строят не нульмерный протяженный объект или просто утверждают, что это – два разных математических объекта, как в геометрии Эвклида точка и прямая. Но о нем забывают, когда применяют геометрические построения и преобразования к реальному пространству и движению. Все дело в том, что мощность непрерывного множества больше, чем дискретного. Иначе говоря, сколько математических точек не ставь, никогда не получишь непрерывную линию. Это противоречие свойственно для всех хаусдорфовых пространств, к которым относятся все метрические и метризуемые пространства, в том числе евклидовое.
Противоречия математической модели реальности наиболее ярко были сформулированы в апориях Зенона, например, касающихся бесконечной делимости пространства. Мы до сих пор пользуемся математическими моделями движения, основанными на геометрии, созданной еще в V веке до н. э. Эта геометрия опиралась на такие понятия, как тело, поверхность, фигура, линия — и на понятие точки пространства, не имеющей никаких собственных измеримых характеристик. То есть мы до сих пор пользуемся моделью классической кривой, которая считается одновременно и непрерывной, и состоящей из бесконечного количества отдельных точек. В математике это противоречие решается либо через монадологию Лейбница, получившую второе рождение в нестандартном анализе, разработанном Абрахам Робинсон в XX веке, либо через подход, предложенный Коши в XIX веке с использованием понятия предела. Но к реальному движению второй подход не имеет отношения. Это – чисто математический приём. Он не разрешает апории Зенона, который как раз ставит под сомнение не логику математической модели, а применимость ее к реальному движению.
То, что проблема математической модели реальности не решена, понимали все ведущие математики и физики XX века.
Так Гильберт и Бернайс высказывали мнение о неадекватности непрерывной, бесконечно делимой математической модели физически дискретной материи. Они отмечали: «мы вовсе не обязательно должны верить в то, что математическое пространственно-временное представление движения имеет физическое значение для произвольно малых интервалов пространства и времени».[1]
Николя Бурбаки писал: «Вопрос о бесконечной делимости пространства (бесспорно, поставленный ещё ранними пифагорейцами) привёл, как известно, к значительным затруднениям в философии: от Элеатов до Больцано и Кантора математики и философы не в силах были разрешить парадокса — как конечная величина может состоять из бесконечного числа точек, не имеющих размера.» [2]
А Ричард Фейнман даже заявил: «Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что [в квантовой механике] она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны.» [3]
Наличие этих противоречий означает, что не верна и аксиома Архимеда, которая гласит, что если есть прямая и на ней обозначены два отрезка а и b с началом в одной точке, причем а
[Error: Irreparable invalid markup ('<b,>') in entry. Owner must fix manually. Raw contents below.]
<div style="text-align: right;"><i>Итак будьте совершенны,
как совершенен Отец ваш Небесный
(Мф. 5:48)</i></div>
<b>Введение</b>
Удивительно устроено познание человека. Даже когда набирается множество фактов, противоречащих или изменяющих выбранную человеком картину мира, он продолжает упорно следовать отжившей модели, не замечая того, что его усилия напрасны. Вместо того, чтобы повернуть, вернуться назад, осмыслить новые данные, изменить вектор движения, он начинает биться в гносеологическую стену в надежде ее проломить. А для оправдания этого безсмысленного действа он придумывает разные причины, модели, которые превращают эту гносеологическую стену либо в непреодолимое препятствие, либо в ничто, тем самым порождая надежду на осмысленность усилий. Человек либо успокаивается, и познание умирает, либо он превращается в пророка, свет истины которого не понимают окружающие.
Наглядный пример тому понимание и применение модели точки. А, по сути, это вопрос о правомерности используемых геометрических моделей, правил их преобразований, о границах применимости моделей действительности.
Если не понимать границ применимости моделей, то мы получаем такие абстракции, которые не только не ведут к истине, но уводят от нее.
<lj-cut>
Эквилибристика ума при решении тех или иных задач математики должна восприниматься только как эквилибристика ума, если в условиях задачи не оговорены граничные условия применения метода.
Например, представление о точке, как нульмерном объекте, сопряжено с противоречием непрерывности линии, которая состоит из множества точек. Это противоречие, например, приводит к тому, что отрезки разной длины по количеству точек равны между собой.
Поясню на примере.
Для этого нарисуем угол и две параллельные секущие. А, В, С, D – точки пересечения секущих со сторонами угла.
<img alt="" height="755" src='https://ic.pics.livejournal.com/matveychev_oleg/27303223/30663300/30663300_original.jpg' width="600" />
Через точки F и H на этих секущих проведем линию ОО’.
Тогда имеем следующую проблему.
Для любой точки на отрезке AF и на отрезке CH <b>всегда</b> найдется такая точка, что через них и точку О можно будет провести прямую. Иначе говоря, как бы, количество точек на AF и CH одинаково. Множества их равномощны, т.е. между точками этих двух отрезков можно установить взаимно однозначное соответствие. Но это будет справедливо для любого отрезка на любой секущей проведенной как угодно близко к точке О. С точки зрения счетных множеств длина AF равна CH. Этот наглядный парадокс, конечно, проистекает из противоречия в аксиоматике, когда из нульмерных непротяженных объектов, каким является математическая точка, строят не нульмерный протяженный объект или просто утверждают, что это – два разных математических объекта, как в геометрии Эвклида точка и прямая. Но о нем забывают, когда применяют геометрические построения и преобразования к реальному пространству и движению. Все дело в том, что мощность непрерывного множества больше, чем дискретного. Иначе говоря, сколько математических точек не ставь, никогда не получишь непрерывную линию. Это противоречие свойственно для всех хаусдорфовых пространств, к которым относятся все метрические и метризуемые пространства, в том числе евклидовое.
Противоречия математической модели реальности наиболее ярко были сформулированы в апориях Зенона, например, касающихся бесконечной делимости пространства. Мы до сих пор пользуемся математическими моделями движения, основанными на геометрии, созданной еще в V веке до н. э. Эта геометрия опиралась на такие понятия, как тело, поверхность, фигура, линия — и на понятие точки пространства, не имеющей никаких собственных измеримых характеристик. То есть мы до сих пор пользуемся моделью классической кривой, которая считается одновременно и непрерывной, и состоящей из бесконечного количества отдельных точек. В математике это противоречие решается либо через монадологию Лейбница, получившую второе рождение в нестандартном анализе, разработанном Абрахам Робинсон в XX веке, либо через подход, предложенный Коши в XIX веке с использованием понятия предела. Но к реальному движению второй подход не имеет отношения. Это – чисто математический приём. Он не разрешает апории Зенона, который как раз ставит под сомнение не логику математической модели, а применимость ее к реальному движению.
То, что проблема математической модели реальности не решена, понимали все ведущие математики и физики XX века.
Так Гильберт и Бернайс высказывали мнение о неадекватности непрерывной, бесконечно делимой математической модели физически дискретной материи. Они отмечали: «мы вовсе не обязательно должны верить в то, что математическое пространственно-временное представление движения имеет физическое значение для произвольно малых интервалов пространства и времени».[1]
Николя Бурбаки писал: «Вопрос о бесконечной делимости пространства (бесспорно, поставленный ещё ранними пифагорейцами) привёл, как известно, к значительным затруднениям в философии: от Элеатов до Больцано и Кантора математики и философы не в силах были разрешить парадокса — как конечная величина может состоять из бесконечного числа точек, не имеющих размера.» [2]
А Ричард Фейнман даже заявил: «Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что [в квантовой механике] она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны.» [3]
Наличие этих противоречий означает, что не верна и аксиома Архимеда, которая гласит, что если есть прямая и на ней обозначены два отрезка а и b с началом в одной точке, причем а <b, a="" b="" b.="" n=""> b.
Это также означает, что дифференциальное исчисление, в котором приращение аргумента стремится к нулю (ньютоновская версия), содержит в себе неразрешимое противоречие. Мы это противоречие просто не хотим видеть, поскольку при определенных размерах исследуемых областей вычисления дают результаты близкие к экспериментальным. Мы перескакиваем через проблему путем различных математических манипуляций, как, например, процесс перенормировки в квантовой электродинамике. В результате укореняется модель, которая дает результаты, но у которой нет объяснений. Это как птолемеевская модель солнечной системы: вычисления дают правильные результат, но к реальной солнечной системе эта модель не имеет отношения.
Сейчас модель точки переживает кризис, когда очевидно, что предыдущая модель работает, но реальность иная и требует кардинально иной модели. Впереди всеобщая «коперниканская» революция модели пространства.
Но кому это интересно, если можно продолжать заниматься эквилибристикой ума, рассуждать об иррациональных числах, которые не имеют никакого отношения к физическому миру. Разве человек (физик, математик и т.д.) может согласиться, что все его труды напрасны? Что все его модели, диссертации, звания и должности основаны на ложном фундаменте? Конечно, нет. Он будет продолжать следовать привычной модели, убеждая себя и других, что в его результатах есть польза, что можно и нужно именно так представлять модель точки, как он привык. А поскольку точка – фундаментальное понятие, то у развития науки появляется огромные тормоз в виде сотен тысяч ученых, наученных и приверженных определенной картине мира, которые будут всячески противиться новому взгляду. Им так проще, им так комфортнее, более хлебно.
Но что же идет на смену математической точки? Физическая. А вместе с ней иная модель пространства, объектов в нем, связей между ними и, конечно, иное представление о человеке и его мышлении.
<span style="font-size:1.4em;">Физическая точка</span>
Наш образ мира сформирован на итерациях от эмпирического факта к модели, от неё к эксперименту и обратно к модели. Именно эксперимент, практика дает нам основания для оценки существующей модели, но в силу ограниченности возможностей человека результаты любого эксперимента предстают в виде конечных чисел, которые относятся к множеству рациональных чисел, т.е. таких, которые можно представить в виде дроби m/n, где числитель m — целое число, а знаменатель n — натуральное число (1,2,3 …). В научных экспериментах мы никогда не имеем дела, например, с бесконечными десятичными дробями, т.е. с иррациональными вещественными числами. При этом трудно себе представить, что когда-то будет такая точность измерений, которая позволит получить бесконечное количество знаком после запятой, т.е. интерпретировать результат, как вещественное число.
Реальным физическим ограничением применимости аксиомы Архимеда являются основания квантовой механики, согласно которой невозможно измерить расстояния меньше планковского, которое задается формулой lpl = √(ħG/c3) ≈1,616 229(38)·10−35 м, где ħ ( h/2π) - постоянная Планка, с – скорость света и G - гравитационная постоянная.
Иначе говоря, согласно принятым геометрическим представлениям, мы должны иметь возможность измерить сколь угодно малые расстояния, но в виду физического ограничения в виде планковской длины в реальном физическом пространстве такое измерение невозможно. Таким образом, мы приходим к выводу, что геометрия риманова пространства неадекватно описывает свойства реального физического пространства на очень малых расстояниях.
Впервые на то, что лишь рациональные числа являются физическими числами, обратили внимание И.В. Волович и В.С. Владимиров.
Но если для описания физического мира отправной точкой следует брать поле рациональных чисел Q, т.е. алгебру, для элементов которой определены операции сложения, вычитания, умножения и деления (кроме деления на нуль), которому соответствует неполное метрическое пространство, то как перейти к математическим моделям таких полей чисел, которым соответствует полное метрическое пространство, т.е. такое, в котором каждая фундаментальная последовательность сходится?
Известно, что геометрическому понятию расстояния между двумя рациональными числами соответствует аналитическое понятие нормы на Q.
Какие же нормы есть на поле рациональных чисел Q?
Удивительно, но согласно теореме Островского их всего две: ||x|| и ||x||р , р =2,3,…, где ||x|| - вещественная норма рационального числа x, а ||x||р - р –адическая норма, которая измеряет, на какую степень p делится рациональное число.
Этими нормами исчерпывают все нетривиальные неэквивалентные нормы поля рациональных чисел Q. Иначе говоря, любая норма на поле рациональных чисел Q эквивалентна либо вещественной норме (обычному абсолютному значению), либо одной из p–адических норм, где р - простое число.
Вещественной нормой рационального числа x называется его модуль |x|, т.е. ||x||=|x|. Полем вещественных (действительных) чисел называется пополнение поля рациональных чисел по вещественной норме, которая удовлетворяет условиям
(1) ||х||≥0, причем ||х||=0 при х=0
(2) ||х•y|| = ||х||•||y||
(3) ||х+y||≤||х|| + ||y||
для любых рациональных чисел х, у.
Р – адической нормой рационального числа х, представленного единственным образом в виде несократимой дроби x =p γ(m/n), где p есть простое число, γ есть целое число, m целое, n натуральное, а p, m, n взаимно просты, называется число
||x||p=p− γ, если x≠0, и 0, если x=0.
Р-адическая норма удовлетворяет следующим условиям
(1) ||х||≥0, причем ||х||=0 при х=0
(2) ||х•y|| = ||х||•||y||
(3') ||х+y||≤ max(||х||p, ||y||p) - усиленное неравенство треугольника
Норма, которая удовлетворяет неравенству (3'), называется неархимедовой.
Пополнение поля рациональных чисел Q по обычной, вещественной норме приводит к полю вещественных чисел R, а пополнение по р-адической норме – к полю р-адических чисел Qp для любого простого р. При этом р-адическое нормирование рациональных чисел является дискретным, т.е. норма может принимать лишь дискретное множество значений, в то время как вещественная норма дает непрерывное множество действительных чисел.
Поля p –адических чисел Qp – единственный примеры неархимедовых числовых полей, получаемых пополнением поля рациональных чисел Q по p–адической норме. После задания метрики dp(x,y)= |x-y|p, x,y ∈ Qр, индуцированной р-адической нормой, Qр становится полным метрическим пространством. Поскольку p–адическая норма неархимедова, то соответствующая ей метрика dp удовлетворяет сильному неравенству треугольника
dp(x,y) ≤ max[dp(x,z)p, dp(z,y)], x,y,z ∈ Qр
Метрика такого типа называется ультраметрикой, а – Qр ультраметрическим пространством для любого р.
Таким образом, модельный мир смотрит на рациональные числа с помощью двух кардинально различных не изоморфных друг другу состояний: поля действительных чисел R и поля р-адических чисел Qр, с уровня непрерывности и уровня дискретности, с точки зрения упорядоченного множества и неупорядоченного, связного и вполне несвязного пространства, пространства с размерностью и имеющего нулевую топологическую размерность, c числовой прямой и c однородного дерева с ветвлением на р частей в каждой вершине.[4]
Важно, что, с одной стороны, метрическое пространство может быть представлено в виде древовидной решетки, а с другой, - подпространство, натянутое на точки, для которых расстояние между ними удовлетворяет усиленному неравенству треугольника, является эвклидовым.
Идея применения р-адических чисел для описания пространства на расстояниях меньше планковского принадлежит В.С. Владимирову и И.В. Воловичу [5- 7].
Эта идея о том, что граница физической точки (если можно говорить о границе) есть граница двух расширений: до множества действительных чисел и до множества р-адических чисел. Если во вне физической точки мы получаем архимедов анализ, то внутри её царствует неархимедов. И что самое важное, согласно теореме Островского, есть только эти два нетривиальных способа расширения множества рациональных чисел.
Таким образом, пространство физической точки – это ультраметрическое пространство, топологическая размерность которого равно нулю.
Но какое отношение все эти построения имеют к человеку?
Для того чтобы ответить на этот вопрос, нужно сначала понять, что из себя представляет ультраметрическое пространство, подобием чего являются его объекты.
Далее <a href="http://www.trinitas.ru/rus/doc/0016/001g/00164260.htm">здесь</a></b,>
</lj-cut>
<lj-like />
<div style="text-align: right;"><i>Итак будьте совершенны,
как совершенен Отец ваш Небесный
(Мф. 5:48)</i></div>
<b>Введение</b>
Удивительно устроено познание человека. Даже когда набирается множество фактов, противоречащих или изменяющих выбранную человеком картину мира, он продолжает упорно следовать отжившей модели, не замечая того, что его усилия напрасны. Вместо того, чтобы повернуть, вернуться назад, осмыслить новые данные, изменить вектор движения, он начинает биться в гносеологическую стену в надежде ее проломить. А для оправдания этого безсмысленного действа он придумывает разные причины, модели, которые превращают эту гносеологическую стену либо в непреодолимое препятствие, либо в ничто, тем самым порождая надежду на осмысленность усилий. Человек либо успокаивается, и познание умирает, либо он превращается в пророка, свет истины которого не понимают окружающие.
Наглядный пример тому понимание и применение модели точки. А, по сути, это вопрос о правомерности используемых геометрических моделей, правил их преобразований, о границах применимости моделей действительности.
Если не понимать границ применимости моделей, то мы получаем такие абстракции, которые не только не ведут к истине, но уводят от нее.
<lj-cut>
Эквилибристика ума при решении тех или иных задач математики должна восприниматься только как эквилибристика ума, если в условиях задачи не оговорены граничные условия применения метода.
Например, представление о точке, как нульмерном объекте, сопряжено с противоречием непрерывности линии, которая состоит из множества точек. Это противоречие, например, приводит к тому, что отрезки разной длины по количеству точек равны между собой.
Поясню на примере.
Для этого нарисуем угол и две параллельные секущие. А, В, С, D – точки пересечения секущих со сторонами угла.
<img alt="" height="755" src='https://ic.pics.livejournal.com/matveychev_oleg/27303223/30663300/30663300_original.jpg' width="600" />
Через точки F и H на этих секущих проведем линию ОО’.
Тогда имеем следующую проблему.
Для любой точки на отрезке AF и на отрезке CH <b>всегда</b> найдется такая точка, что через них и точку О можно будет провести прямую. Иначе говоря, как бы, количество точек на AF и CH одинаково. Множества их равномощны, т.е. между точками этих двух отрезков можно установить взаимно однозначное соответствие. Но это будет справедливо для любого отрезка на любой секущей проведенной как угодно близко к точке О. С точки зрения счетных множеств длина AF равна CH. Этот наглядный парадокс, конечно, проистекает из противоречия в аксиоматике, когда из нульмерных непротяженных объектов, каким является математическая точка, строят не нульмерный протяженный объект или просто утверждают, что это – два разных математических объекта, как в геометрии Эвклида точка и прямая. Но о нем забывают, когда применяют геометрические построения и преобразования к реальному пространству и движению. Все дело в том, что мощность непрерывного множества больше, чем дискретного. Иначе говоря, сколько математических точек не ставь, никогда не получишь непрерывную линию. Это противоречие свойственно для всех хаусдорфовых пространств, к которым относятся все метрические и метризуемые пространства, в том числе евклидовое.
Противоречия математической модели реальности наиболее ярко были сформулированы в апориях Зенона, например, касающихся бесконечной делимости пространства. Мы до сих пор пользуемся математическими моделями движения, основанными на геометрии, созданной еще в V веке до н. э. Эта геометрия опиралась на такие понятия, как тело, поверхность, фигура, линия — и на понятие точки пространства, не имеющей никаких собственных измеримых характеристик. То есть мы до сих пор пользуемся моделью классической кривой, которая считается одновременно и непрерывной, и состоящей из бесконечного количества отдельных точек. В математике это противоречие решается либо через монадологию Лейбница, получившую второе рождение в нестандартном анализе, разработанном Абрахам Робинсон в XX веке, либо через подход, предложенный Коши в XIX веке с использованием понятия предела. Но к реальному движению второй подход не имеет отношения. Это – чисто математический приём. Он не разрешает апории Зенона, который как раз ставит под сомнение не логику математической модели, а применимость ее к реальному движению.
То, что проблема математической модели реальности не решена, понимали все ведущие математики и физики XX века.
Так Гильберт и Бернайс высказывали мнение о неадекватности непрерывной, бесконечно делимой математической модели физически дискретной материи. Они отмечали: «мы вовсе не обязательно должны верить в то, что математическое пространственно-временное представление движения имеет физическое значение для произвольно малых интервалов пространства и времени».[1]
Николя Бурбаки писал: «Вопрос о бесконечной делимости пространства (бесспорно, поставленный ещё ранними пифагорейцами) привёл, как известно, к значительным затруднениям в философии: от Элеатов до Больцано и Кантора математики и философы не в силах были разрешить парадокса — как конечная величина может состоять из бесконечного числа точек, не имеющих размера.» [2]
А Ричард Фейнман даже заявил: «Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что [в квантовой механике] она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны.» [3]
Наличие этих противоречий означает, что не верна и аксиома Архимеда, которая гласит, что если есть прямая и на ней обозначены два отрезка а и b с началом в одной точке, причем а <b, a="" b="" b.="" n=""> b.
Это также означает, что дифференциальное исчисление, в котором приращение аргумента стремится к нулю (ньютоновская версия), содержит в себе неразрешимое противоречие. Мы это противоречие просто не хотим видеть, поскольку при определенных размерах исследуемых областей вычисления дают результаты близкие к экспериментальным. Мы перескакиваем через проблему путем различных математических манипуляций, как, например, процесс перенормировки в квантовой электродинамике. В результате укореняется модель, которая дает результаты, но у которой нет объяснений. Это как птолемеевская модель солнечной системы: вычисления дают правильные результат, но к реальной солнечной системе эта модель не имеет отношения.
Сейчас модель точки переживает кризис, когда очевидно, что предыдущая модель работает, но реальность иная и требует кардинально иной модели. Впереди всеобщая «коперниканская» революция модели пространства.
Но кому это интересно, если можно продолжать заниматься эквилибристикой ума, рассуждать об иррациональных числах, которые не имеют никакого отношения к физическому миру. Разве человек (физик, математик и т.д.) может согласиться, что все его труды напрасны? Что все его модели, диссертации, звания и должности основаны на ложном фундаменте? Конечно, нет. Он будет продолжать следовать привычной модели, убеждая себя и других, что в его результатах есть польза, что можно и нужно именно так представлять модель точки, как он привык. А поскольку точка – фундаментальное понятие, то у развития науки появляется огромные тормоз в виде сотен тысяч ученых, наученных и приверженных определенной картине мира, которые будут всячески противиться новому взгляду. Им так проще, им так комфортнее, более хлебно.
Но что же идет на смену математической точки? Физическая. А вместе с ней иная модель пространства, объектов в нем, связей между ними и, конечно, иное представление о человеке и его мышлении.
<span style="font-size:1.4em;">Физическая точка</span>
Наш образ мира сформирован на итерациях от эмпирического факта к модели, от неё к эксперименту и обратно к модели. Именно эксперимент, практика дает нам основания для оценки существующей модели, но в силу ограниченности возможностей человека результаты любого эксперимента предстают в виде конечных чисел, которые относятся к множеству рациональных чисел, т.е. таких, которые можно представить в виде дроби m/n, где числитель m — целое число, а знаменатель n — натуральное число (1,2,3 …). В научных экспериментах мы никогда не имеем дела, например, с бесконечными десятичными дробями, т.е. с иррациональными вещественными числами. При этом трудно себе представить, что когда-то будет такая точность измерений, которая позволит получить бесконечное количество знаком после запятой, т.е. интерпретировать результат, как вещественное число.
Реальным физическим ограничением применимости аксиомы Архимеда являются основания квантовой механики, согласно которой невозможно измерить расстояния меньше планковского, которое задается формулой lpl = √(ħG/c3) ≈1,616 229(38)·10−35 м, где ħ ( h/2π) - постоянная Планка, с – скорость света и G - гравитационная постоянная.
Иначе говоря, согласно принятым геометрическим представлениям, мы должны иметь возможность измерить сколь угодно малые расстояния, но в виду физического ограничения в виде планковской длины в реальном физическом пространстве такое измерение невозможно. Таким образом, мы приходим к выводу, что геометрия риманова пространства неадекватно описывает свойства реального физического пространства на очень малых расстояниях.
Впервые на то, что лишь рациональные числа являются физическими числами, обратили внимание И.В. Волович и В.С. Владимиров.
Но если для описания физического мира отправной точкой следует брать поле рациональных чисел Q, т.е. алгебру, для элементов которой определены операции сложения, вычитания, умножения и деления (кроме деления на нуль), которому соответствует неполное метрическое пространство, то как перейти к математическим моделям таких полей чисел, которым соответствует полное метрическое пространство, т.е. такое, в котором каждая фундаментальная последовательность сходится?
Известно, что геометрическому понятию расстояния между двумя рациональными числами соответствует аналитическое понятие нормы на Q.
Какие же нормы есть на поле рациональных чисел Q?
Удивительно, но согласно теореме Островского их всего две: ||x|| и ||x||р , р =2,3,…, где ||x|| - вещественная норма рационального числа x, а ||x||р - р –адическая норма, которая измеряет, на какую степень p делится рациональное число.
Этими нормами исчерпывают все нетривиальные неэквивалентные нормы поля рациональных чисел Q. Иначе говоря, любая норма на поле рациональных чисел Q эквивалентна либо вещественной норме (обычному абсолютному значению), либо одной из p–адических норм, где р - простое число.
Вещественной нормой рационального числа x называется его модуль |x|, т.е. ||x||=|x|. Полем вещественных (действительных) чисел называется пополнение поля рациональных чисел по вещественной норме, которая удовлетворяет условиям
(1) ||х||≥0, причем ||х||=0 при х=0
(2) ||х•y|| = ||х||•||y||
(3) ||х+y||≤||х|| + ||y||
для любых рациональных чисел х, у.
Р – адической нормой рационального числа х, представленного единственным образом в виде несократимой дроби x =p γ(m/n), где p есть простое число, γ есть целое число, m целое, n натуральное, а p, m, n взаимно просты, называется число
||x||p=p− γ, если x≠0, и 0, если x=0.
Р-адическая норма удовлетворяет следующим условиям
(1) ||х||≥0, причем ||х||=0 при х=0
(2) ||х•y|| = ||х||•||y||
(3') ||х+y||≤ max(||х||p, ||y||p) - усиленное неравенство треугольника
Норма, которая удовлетворяет неравенству (3'), называется неархимедовой.
Пополнение поля рациональных чисел Q по обычной, вещественной норме приводит к полю вещественных чисел R, а пополнение по р-адической норме – к полю р-адических чисел Qp для любого простого р. При этом р-адическое нормирование рациональных чисел является дискретным, т.е. норма может принимать лишь дискретное множество значений, в то время как вещественная норма дает непрерывное множество действительных чисел.
Поля p –адических чисел Qp – единственный примеры неархимедовых числовых полей, получаемых пополнением поля рациональных чисел Q по p–адической норме. После задания метрики dp(x,y)= |x-y|p, x,y ∈ Qр, индуцированной р-адической нормой, Qр становится полным метрическим пространством. Поскольку p–адическая норма неархимедова, то соответствующая ей метрика dp удовлетворяет сильному неравенству треугольника
dp(x,y) ≤ max[dp(x,z)p, dp(z,y)], x,y,z ∈ Qр
Метрика такого типа называется ультраметрикой, а – Qр ультраметрическим пространством для любого р.
Таким образом, модельный мир смотрит на рациональные числа с помощью двух кардинально различных не изоморфных друг другу состояний: поля действительных чисел R и поля р-адических чисел Qр, с уровня непрерывности и уровня дискретности, с точки зрения упорядоченного множества и неупорядоченного, связного и вполне несвязного пространства, пространства с размерностью и имеющего нулевую топологическую размерность, c числовой прямой и c однородного дерева с ветвлением на р частей в каждой вершине.[4]
Важно, что, с одной стороны, метрическое пространство может быть представлено в виде древовидной решетки, а с другой, - подпространство, натянутое на точки, для которых расстояние между ними удовлетворяет усиленному неравенству треугольника, является эвклидовым.
Идея применения р-адических чисел для описания пространства на расстояниях меньше планковского принадлежит В.С. Владимирову и И.В. Воловичу [5- 7].
Эта идея о том, что граница физической точки (если можно говорить о границе) есть граница двух расширений: до множества действительных чисел и до множества р-адических чисел. Если во вне физической точки мы получаем архимедов анализ, то внутри её царствует неархимедов. И что самое важное, согласно теореме Островского, есть только эти два нетривиальных способа расширения множества рациональных чисел.
Таким образом, пространство физической точки – это ультраметрическое пространство, топологическая размерность которого равно нулю.
Но какое отношение все эти построения имеют к человеку?
Для того чтобы ответить на этот вопрос, нужно сначала понять, что из себя представляет ультраметрическое пространство, подобием чего являются его объекты.
Далее <a href="http://www.trinitas.ru/rus/doc/0016/001g/00164260.htm">здесь</a></b,>
</lj-cut>
<lj-like />
Свежие комментарии