Пятисторонний квадрат

Совсем не сложный вопрос, что такое квадрат? 

Квадрат в евклидовой геометрии - правильный четырёхугольник, у которого все стороны равны и углы прямые. 

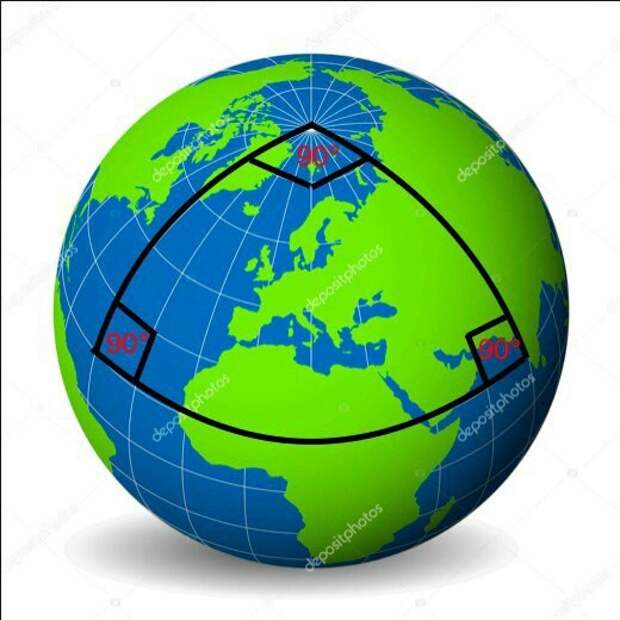
Мы знаем, что угол между меридианом и экватором равен 90°, тогда, если подняться вверх по меридиану к вершине шарового сегмента, пусть это будет т.

М, то существует угол, равный 1/4 от окружности верхнего сегмента (90°) и опуститься вниз к экватору, где угол так же равен 90°, мы получаем равносторонний треугольник с суммой углов больше 180°. Нарисовав любой треугольник на сфере, сумма его углов будет больше 180°. Если говорить, что в альтернативной геометрии квадрат - это фигура с равными сторонами и прямыми углами, то из определения квадрата можно сделать вывод, что это трёхсторонний квадрат (все стороны равны и все углы прямые). Корректно выражаясь, это будет не совсем так. 

Немного о сферической тригонометрии 

Сферическая тригонометрия – это такой раздел тригонометрии, в котором изучаются зависимости между величинами углов и длинами сторон сферических треугольников. Применяется для решения различных геодезических и астрономических задач.

В такой тригонометрии вершинами сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара, и сферической поверхности. Каждая сторона и угол сфери¬ческого треугольника по определению мень¬ше 180°. Тригонометрия на сфере не относится к евклидовой. Сумма сторон в таком треугольнике находиться в диапазоне от 0° до 360°, а сумма углов - 180° и 540°. Против большей стороны лежит больший угол сферического треугольника.

Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180° плюс третий угол.

Углубимся еще немножко 
Гауссова кривизна — мера искривления поверхности в окрестности какой-либо её точки. Гауссова кривизна является объектом внутренней геометрии поверхностей, в частности, не изменяется при изометрических изгибаниях. 
Сфера - основной пример фигуры с постоянной положительной кривизной 
Это означает, что, проведя через любую точку на сфере две кривые, они будут положительной кривизны (обе кривые будут выгнутыми наружу). 

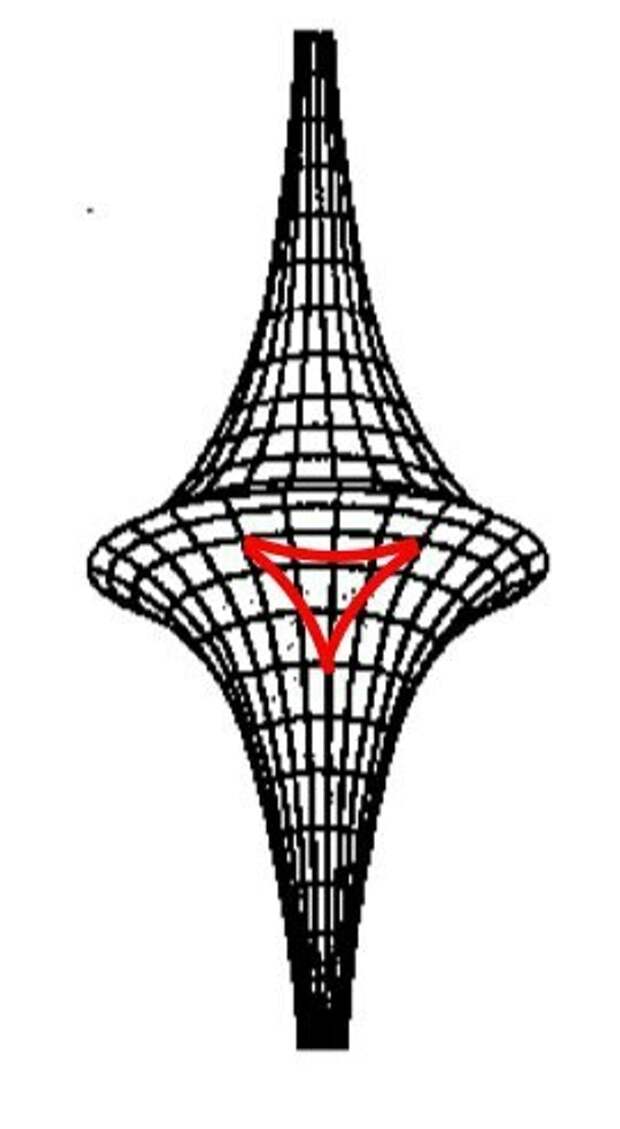
Тогда возникает вопрос, а есть ли фигуры с постоянной отрицательной кривизной? Раз уж заговорили, то да, они есть. Можно привести пример на основе псевдосферы (поверхности Бельтрами). Это поверхность с постоянной отрицательной кривизной, при условии, что мы возьмём минимум вогнутости и максимум выпуклости или одно из них. Нарисовав любой треугольник на псевдосфере, сумма его углов будет меньше 180°. 

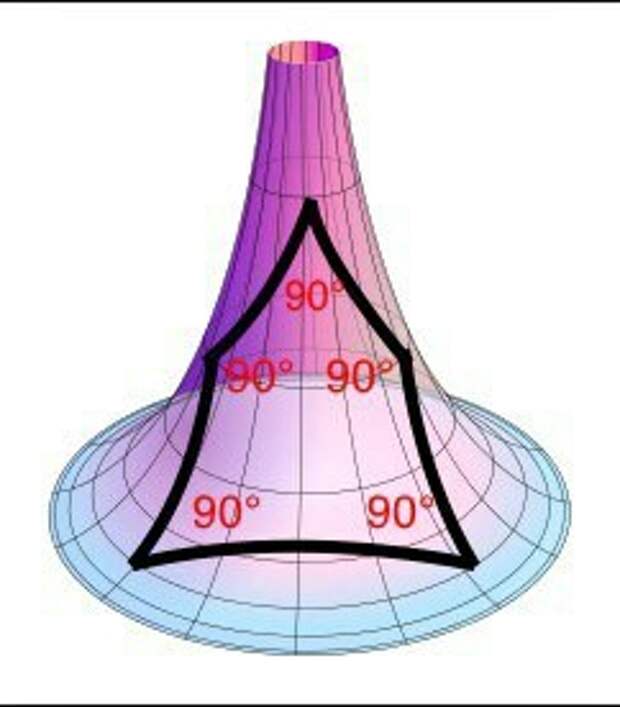
Соединив определённым образом равносторонние лучи под прямым углом мы можем получить 5-и стороннюю фигуру с равными сторонами и всеми прямыми углами. Таким образом можно получить на псевдосфере пятисторонний квадрат.

Спасибо за внимание.